Relative Frequency And Cumulative Frequency

Cumulative frequency

Archived Content

Information identified as archived is provided for reference, research or recordkeeping purposes. It is not subject to the Regime of Canada Spider web Standards and has not been altered or updated since it was archived. Please contact us to request a format other than those available.

Instance 1 – Discrete variables
Example 2 – Continuous variables
Other cumulative frequency calculations

Cumulative frequency is used to determine the number of observations that lie above (or below) a item value in a data prepare. The cumulative frequency is calculated using a frequency distribution table, which tin be constructed from stem and foliage plots or straight from the information.

The cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors. The last value will ever exist equal to the total for all observations, since all frequencies will already take been added to the previous total.

Discrete or continuous variables

Variables in any adding can be characterized by the value assigned to them. A discrete variable consists of separate, indivisible categories. No values can be between a variable and its neighbour. For instance, if you were to observe a form attendance registered from day-to-day, yous may find that the class has 29 students on one day and 30 students on another. However, it is incommunicable for student attendance to exist between 29 and xxx. (In that location is simply no room to find any values between these two values, as there is no way of having 29 and a one-half students.)

Not all variables are characterized as discrete. Some variables (such every bit time, meridian and weight) are non limited to a fixed prepare of indivisible categories. These variables are called continuous variables, and they are divisible into an infinite number of possible values. For case, time tin can be measured in partial parts of hours, minutes, seconds and milliseconds. So, instead of finishing a race in 11 or 12 minutes, a jockey and his horse can cross the finish line at 11 minutes and 43 seconds.

It is essential to know the difference between the two types of variables in club to properly summate their cumulative frequency.

Top of Page

Example 1 – Discrete variables

The total rock climber count of Lake Louise, Alberta was recorded over a thirty-day menses. The results are as follows:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, iv, 54, 39, 52, 35, 51, 63, 42.

Utilize these discrete variables to:
- gear up a stem and leafage plot, (encounter the section on stem and leaf plots) with boosted columns labelled Frequency, Upper Value and Cumulative frequency
- effigy out the frequency of observations for each stem
- find the upper value for each stalk
- calculate the cumulative frequency by adding the numbers in the Frequency cavalcade
- record all the results in the plot
Plot a graph using the y-axis (or vertical line) for the cumulative frequency and the ten-centrality (or horizontal line) for the number of people rock climbing.

Answers:

The number of rock climbers ranges from iv to 65. In guild to produce a stem and leaf plot, the data are best grouped in class intervals of ten.

Each interval can be located in the Stem column. The numbers within this column represent the first number within the class interval. (For example, Stalk 0 represents the interval 0–9, Stalk 1 represents the interval of 10–19, and and then forth.)

The Leaf cavalcade lists the number of observations that lie within each grade interval. For case, in Stem 2 (interval 20–29), the iii observations, 23, 24, and 26, are represented every bit 3, 4 and 6.

The Frequency column lists the number of observations plant within a class interval. For instance, in Stem 5, nine leaves (or observations) were found; in Stem ane, there are only two.

Use the Frequency cavalcade to summate cumulative frequency.

Outset, add together the number from the Frequency column to its predecessor. For example, in Stalk 0, we take merely one observation and no predecessors. The cumulative frequency is one.
i + 0 = i
Nevertheless in Stalk i, there are two observations. Add these two to the previous cumulative frequency (one), and the result is three.
one + 2 = 3
In Stalk 2, there are three observations. Add together these three to the previous cumulative frequency (iii) and the total (vi) is the cumulative frequency for Stalk two.
3 + 3 = vi
Go along these calculations until you have added up all of the numbers in the Frequency cavalcade.
Record the results in the Cumulative frequency column.

The Upper value column lists the observation (variable) with the highest value in each of the class intervals. For example, in Stem ane, the ii observations 8 and 9 correspond the variables 18 and 19. The upper value of these ii variables is 19.

Table 1. Cumulative frequency of daily stone climber counts recorded in Lake Louise, Alberta, xxx-day period
Stem	Leaf	Frequency (f)	Upper value	Cumulative frequency
0	four	1	4	1
1	8 9	two	19	one + 2 = 3
2	3 4 six	iii	26	3 + 3 = 6
three	1 5 5 vii 9	5	39	half dozen + v = 11
4	0 one 2 3 5 nine	vi	49	11 + 6 = 17
5	0 1 1 two 4 iv v 6 7	9	57	17 + 9 = 26
half dozen	0 two iii 5	iv	65	26 + 4 = 30

Since these variables are detached, employ the upper values in plotting the graph. Plot the points to form a continuous curve called an ogive.
Always characterization the graph with the cumulative frequency—corresponding to the number of observations made—on the vertical centrality. Label the horizontal axis with the other variable (in this instance, the total rock climber counts) as shown below:

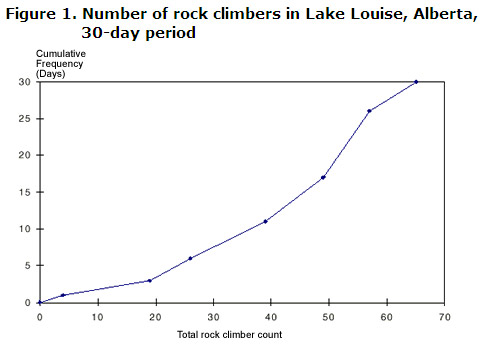
The post-obit information can exist gained from either graph or table:

on 11 of the 30 days, 39 people or fewer climbed the rocks around Lake Louise
on 13 of the 30 days, 50 or more people climbed the rocks around Lake Louise

When a continuous variable is used, both calculating the cumulative frequency and plotting the graph require a slightly different arroyo from that used for a discrete variable.

Superlative of Page

Instance 2 – Continuous variables

For 25 days, the snow depth at Whistler Mountain, B.C. was measured (to the nearest centimetre) and recorded equally follows:

242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.

Apply the continuous variables above to:
- set up a frequency distribution table
- discover the frequency for each class interval
- locate the endpoint for each course interval
- calculate the cumulative frequency by adding the numbers in the Frequency cavalcade
- record all results in the table
Use the data gathered from the frequency distribution tabular array to plot a cumulative frequency graph.

Answers:

The snow depth measurements range from 209 cm to 266 cm. In order to produce the frequency distribution table, the information are best grouped in course intervals of x cm each.

In the Snow depth column, each 10-cm course interval from 200 cm to 270 cm is listed.

The Frequency cavalcade records the number of observations that fall within a particular interval. This column represents the observations in the Tally column, just in numerical form.

The Endpoint column functions much similar the Upper value column of Exercise ane, with the exception that the endpoint is the highest number in the interval, regardless of the actual value of each ascertainment. For example, in the course interval of 210–220, the actual value of the two observations is 217 and 219. But, instead of using 219, the endpoint of 220 is used.

The Cumulative frequency column lists the total of each frequency added to its predecessor.

Table ii. Snow depth measured at Whistler Mount, B.C., 25-day period
Snow depth (x)	Frequency (f)	Endpoint	Cumulative frequency
		200	0
200 to < 210	ane	210	one
210 to < 220	two	220	3
220 to < 230	3	230	half dozen
230 to < 240	v	240	11
240 to < 250	7	250	18
250 to < 260	5	260	23
260 to < 270	2	270	25

Because the variable is continuous, the endpoints of each class interval are used in plotting the graph. The plotted points are joined to form an ogive.
Remember, the cumulative frequency (number of observations made) is labelled on the vertical y-centrality and any other variable (snowfall depth) is labelled on the horizontal 10-axis as shown in Figure 2.

The following information can be gained from either graph or tabular array:

none of the 25 days had snowfall depth less than 200 cm
one of the 25 days snowfall had depth of less than 210 cm
ii of the 25 days snow had depth 260 cm or more

Top of Page

Other cumulative frequency calculations

Some other calculation that can be obtained using a frequency distribution table is the relative frequency distribution. This method is defined as the percent of observations falling in each grade interval. Relative cumulative frequency tin be plant past dividing the frequency of each interval by the full number of observations. (For more data, see Frequency distribution in the chapter entitled Organizing data.)

A frequency distribution table tin also exist used to calculate cumulative percentage. This method of frequency distribution gives us the percentage of the cumulative frequency, equally opposed to the percent of just the frequency.